LaSO--Label-Set Operations networks for multi-lable few-shot learning

0.LaSO: Label-Set Operations networks for multi-lable few-shot learning

1. Summary

This paper focus on the multi-label few-shot learning, where has no prior work of this task. They proposed Label-Set Operations networks, which can generate new multi-label samples in the feature space, this method can be seen as data augmentation techinques.

2. Research Objective

• Find a method to solve the multi-label few-shot learning task and demonstrate the its utility for this work.

3. Problem Statement

• It'a combination of multi-lable classfication task and few-shot learning task. It would train the network on the multi-label training set and validate or test it on the dataset which has the catagories unseen during training.
• Need to use the mAP to evaluate the performance.

4. Methods

• Schematic
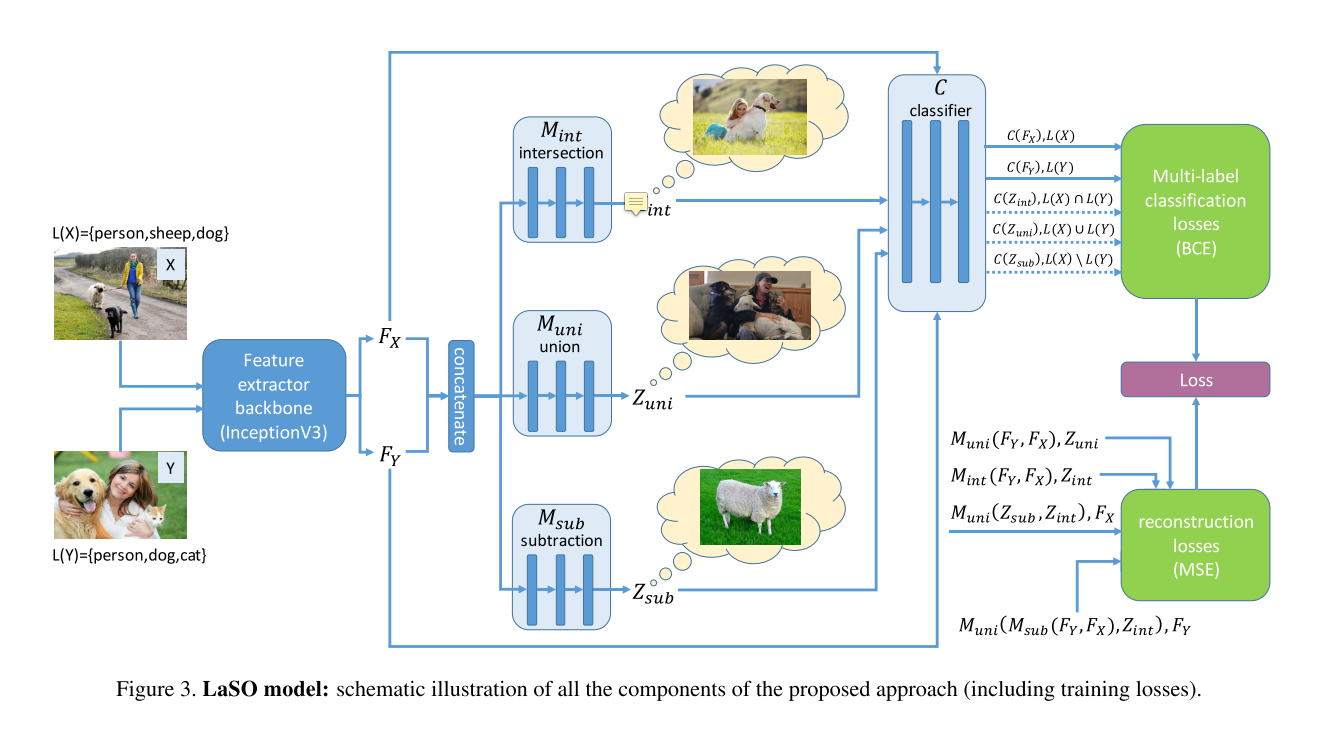
  • feature extractor backbone are pre-trained from training set using networks like InceptonV3, ResNet-34
  • LaSO network are implemented as Multi-Layer Perceptrons consisting of 3 or 4 blocks.
• steps:
  • randomly select a pair of images \(X\) and \(Y\), mapping them into the feature space as \(F_X\) and \(F_Y\). \(X\) and \(Y\) are corresponding set of multiple labels, \(L(X), L(Y) \subseteq\mathcal{L}\)
  • The LaSO network \(M_{int}\), \(M_{uni}\) and \(M_{sub}\) receive the concatenated \(F_X\) and \(F_Y\) and are trained to synthesize feature vectors in the same feature space. That mimic the set operations corresponding intersection, union and subtraction.for example, \(M_{int}(F_X,F_Y)=Z_{int}\in\mathcal{F}\),suppose having generateed a new image \(I\), so the feature vector of \(I\) is \(Z_{int}\), the multi-label of \(I\) is \(L(I)=L(X)\cap L(B)\), same meaning as the two leaving operations.
  • source feature vectors, \(F_X\), \(F_Y\), and the outputs of LaSO networks, namely \(Z_{int}\), \(Z_{uni}\), \(Z_{sub}\) are fed into a classifier \(C\)
• loss function:
  • Need to train two networks, classifier \(C\) and LaSO network. Use the BCE(Binary Cross-Entropy) loss. $BCE(s,l) = -_{i}l_ilog(s_i)+(1-l_i)log(1-(s_i)) $ where vector \(s\) being the classifier scores, \(l\) being the desired(binary) labels vector, and \(i\) the class indices. \(C_{loss}=BCE(C(F_X),L(X))+BCE(C(F_Y),L(Y))\) \(LaSO_{loss} = BCE(C(Z_{int}),L(X)\cap L(Y))+BCE(C(Z_{uni}),L(X)\cup L(Y)) + BCE(C(Z_{sub}), L(X)\setminus L(Y))\) for the LaSO updates the classifier \(C\) is kept fixed and only used for passing gradient backwards.
  • add a set of Mean Square Error based restruction losses. First is used to enforce symmetry for the symmetric intersection and union operation. The second is used to reduce of mode collapse.

5.Evaluate

• use batch size of 16, initial learning rate of 0.001, learning rate reduced on loss plateau with factor 0.3. On all compared approaches the classifier trained on each of the episodes were trained using 40 SGD epochs. Use Adam optimizer with parameters(0.9, 0.999)
• evaluate on two datasets: MS-COCO, CelebA
  
• episode construction: Because each image has multiple labels, so to form a episode, we need to ensure that 1 example per category appears in the episode for 1-shot task and 5 examples category appears in the episode for 5-shot task. Due to the random nature of the episodes, this balancing is not always possible.

6.Conclusion

• LaSO networks can generalize to unseen categories and support their use for performing augmentation synthesis for few-shot multi-label learning

7.Notes

• This paper also evaluate the label set manipulation capability of the LaSO networks, to make sure this manipulation is useful.
• This paper also compare the approximations set operations(without training) with LaSO networks.
• Although it is a few-shot learning task, the datasets used to training are huge(MS-COCO, CelebA)...

8.Reference

• A. J. Ratner, H. R. Ehrenberg, Z. Hussain, J. Dunnmon, and C. R´e. Learning to Compose Domain-Specific Transforma- tions for Data Augmentation. (Nips), 2017.